Combat calculation: a mathematical model predicts the scenario of a military conflict

A mathematician from MIPT has developed a model for predicting the dynamics of modern armed conflicts, which for the first time takes into account a number of parameters related to the movement of troops. It extends the classical Lanchester laws, traditionally used to assess the development of events on the battlefield. In addition, the tool allows you to identify potential hot spots. At the same time, experts note that the simulation results often do not match the real situation and this is influenced by many factors. For more information, see the Izvestia article.

The model as a military analysis tool

A mathematician from MIPT has improved a model for describing the dynamics of modern armed conflicts, which for the first time takes into account the nonlinear dependence of troop movements on their own concentration and the density of enemy forces. As the university's press service explained to Izvestia, back in the early 20th century, Frederick Lanchester derived equations describing losses in battle, and mathematics became an integral tool for military analysis. The simple formulas of the English engineer, linking the number of sides and their combat effectiveness, formed the basis of the theory of operations research.

However, the classic Lanchester models have a significant drawback: they treat armies as homogeneous masses, without taking into account their location and movement on the battlefield, the institute notes. In modern conflicts, where mobility, concentration of forces in key areas and the ability to avoid the environment play a crucial role, this approach is insufficient. The battlefield is a dynamic environment in which the density of troops is constantly changing, affecting their maneuverability and fire efficiency.

To overcome these limitations, Nikita Borisov, a graduate student at the Department of Systems and Solutions Analysis at MIPT, proposed a new approach. He presented the battlefield as a two-dimensional space, at each point of which the density of forces of the two opposing sides is described by a system of reaction-diffusion equations. In this system, in addition to the classical terms of the equation describing losses in combat (reaction), there are also diffusion terms responsible for the movement of troops. The key innovation is that the diffusion coefficient, that is, the "mobility" of troops, is not a constant value. It depends non-linearly on the concentration of both its own and enemy forces.

This approach allows you to model realistic tactical scenarios: for example, a high concentration of your forces can facilitate logistics and increase mobility (the "blitzkrieg effect"), while the presence of the enemy, on the contrary, hinders movement (the "chaining effect").

— As a scientist, I was interested in the problem of creating a mathematical tool that speaks the language of tactics, — said Nikita Borisov. — Instead of abstract numbers, the model uses concepts of concentration of forces, mobility, logistical support, and restricted access zones. Our development shows how these factors interact in space and time, leading to self—organization on the battlefield - the formation of fronts, targeted strikes, breakthroughs and encirclements. This is a step from simple "loss accounting" to full-fledged dynamic simulation of combat operations.

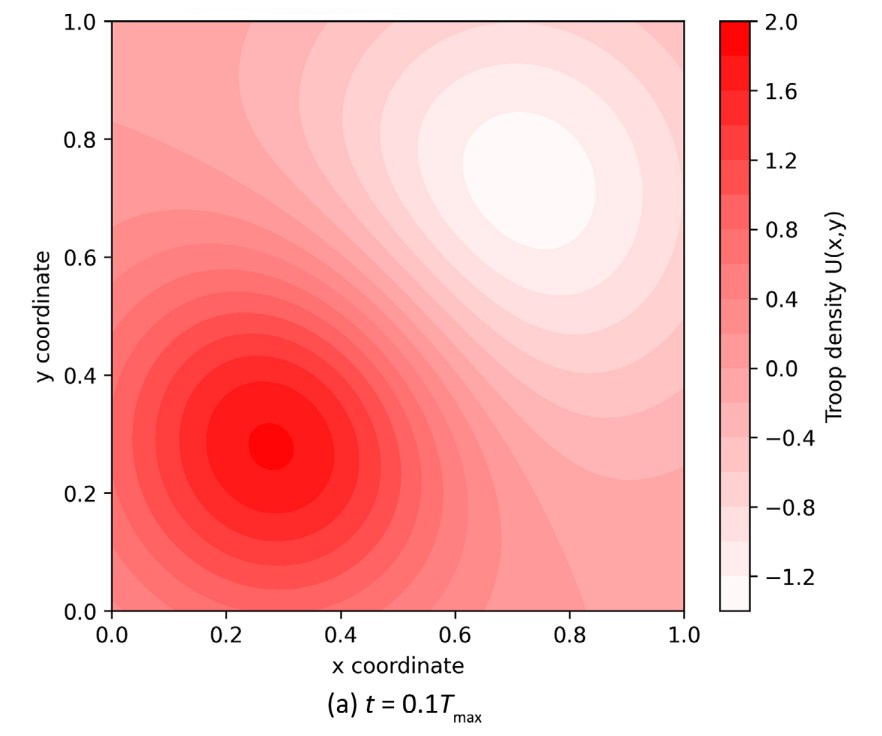
According to the scientists, the proposed model is highly flexible: by changing the parameters, it is possible to simulate various tactical scenarios. The results of the study are applicable to mathematical modeling in military strategy and tactics. The tool allows you to evaluate the effectiveness of the distribution of forces, analyze various combat situations, test new types of weapons and plan logistical operations.

In the future, the author plans to improve the model by adding a three-dimensional space to it to account for aviation and terrain, adaptive time steps, which will further increase its realism and predictive power. Scientists also plan to develop software based on the proposed system.

Creative disruption: the troops began to train sappers-stormtroopers

Specially trained fighters are needed to destroy enemy fortifications.

Why mathematical models can be wrong

The developed model is a generalization of the classical Lanchester equations, which was used for aerial battles during the First World War. In Russian applied science, these equations are also known as the Lanchester—Osipov model (Mikhail Osipov is a general in the Imperial Army of the Russian Empire), Vladimir Nefedov, associate professor at the Faculty of Mechanical Engineering at Lomonosov Moscow State University, told Izvestia.

— This topic is of considerable and ongoing interest. Taking into account the improvement of AI, computer technologies, for example, the possibility of using supercomputers in mathematical analysis, etc. such modeling can and should receive a powerful impetus for development," the scientist said.

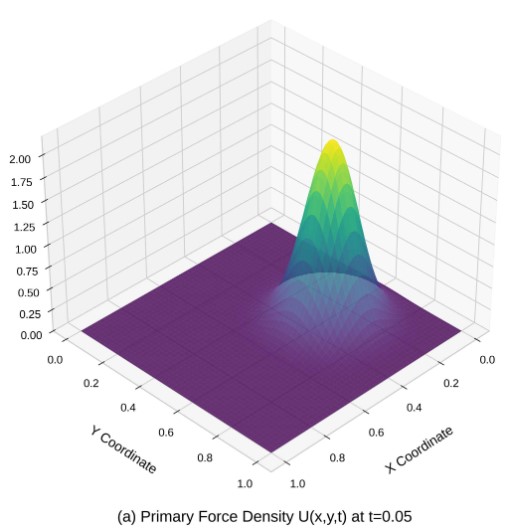
There are alternative approaches used to assess combat operations, and similar studies are being actively conducted both in Russia and abroad, including in the United States, the scientist said.

It is commendable that Russian scientists at the MIPT level are engaged in such important tasks as the development of mathematical models for the spatial interaction of warring groups. The author, starting from the basis, added a spatial component related to the concentration of troops, Dmitry Kuzyakin, chief designer of the Central Design Bureau, told Izvestia.

— It was not necessary to use military themes to describe this mathematical apparatus. One could consider, for example, the interaction of the boundaries of two dynamically active environments. Nevertheless, the author chose armed conflicts," the expert noted. — There are no complaints about the article itself: it is completely scientific. However, the value of mathematical systems is determined by their usefulness and applicability. There are, for example, predictive models that are used to assess the likelihood of customer churn, stock fluctuations, competitor behavior in the market, and other processes.

The expert notes that the mathematical apparatus is scientifically correct in all cases, but in practice it does not always work. Any models or combinations of them are not able to give a statistically significant result, the expert is sure. The reasons are different: the first is the influence of the model itself on the emerging reality; the second is the appearance of unexpected factors, the so—called "black swans", for example, FPV drones on the battlefield.

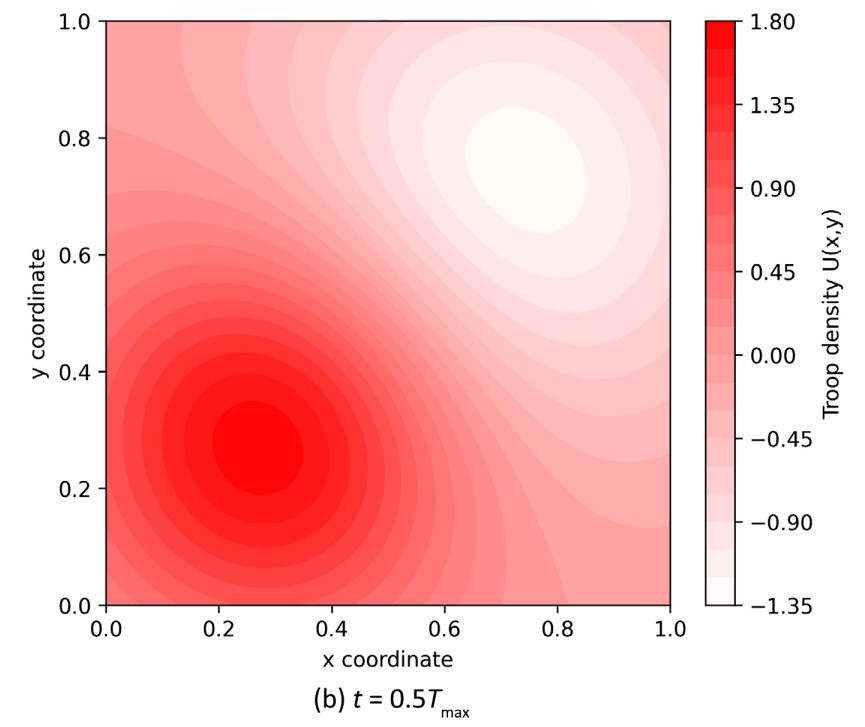
— The academic value of the proposed solution is that it is not contradictory and mathematically pure. The practical one requires verification," Dmitry Kuzyakin summed up.

The results of the study are published in the Journal of Applied Mathematics and Physics.